Derivatans definition kan sägas vara ett gränsvärde där vi låter en sekant gå mot att bli en tangent. Man skriver gränsvärdet på följande vis:
\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}
Om vi ritar ut detta i en graf så ser det ut på följande vis
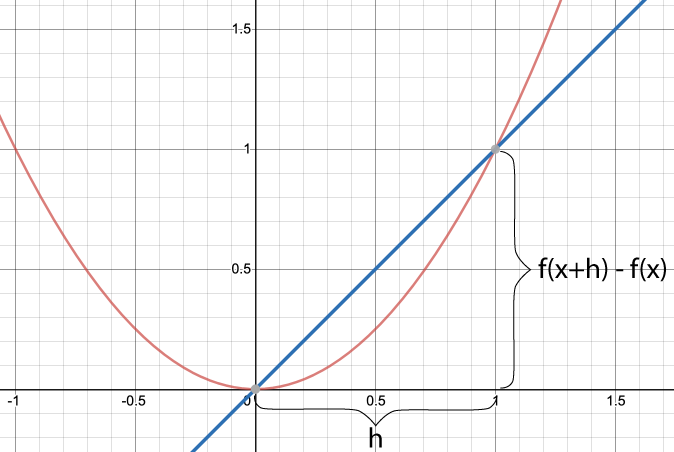
I bilden är en sekant utritad. Lutningen på sekanten får vi genom
\frac{f(x+h)-f(x)}{h}Innebörden av lutningen är den genomsnittliga förändringshastigheten i intervallet. Jämför gärna det med medelhastighet.
Om vi istället vill få lutningen i en punkt kan vi låta h gå mot 0. Då kommer vi istället få tangentens lutning. Därför kan vi rita ut hur det ser ut när h går mot 0 och sekanten går mot att vara en tangent istället.
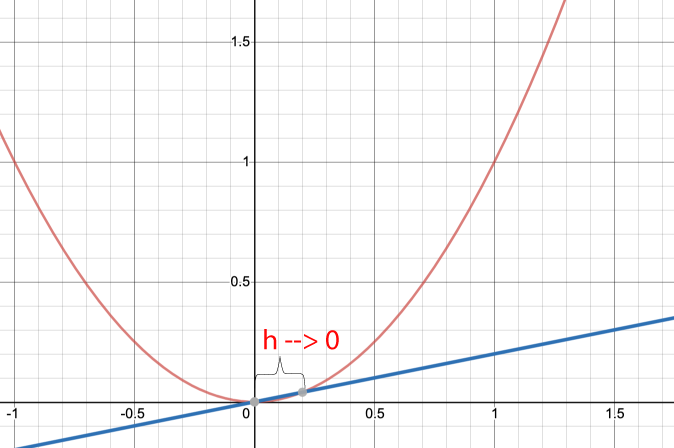
Vi låter alltså h gå mot noll och istället får vi lutningen i en punkt. Vi får då förändringshastigheten i en punkt. Med det menas att vi får förändringen vid en specifik tidpunkt. Det är det som derivata innebär!
Exempel på att använda derivatans definition
Bestäm derivatan för f(x) = x^2 med hjälp av derivatans definition.
Vi ställer upp gränsvärdet
\lim\limits_{h \to 0} \frac{f(x+h)-f(x)}{h}Vi sätter in detta i funktionen f(x) = x^2
\lim\limits_{h \to 0} \frac{(x+h)^2-x^2}{h}Utveckla kvadraten
\lim\limits_{h \to 0} \frac{x^2+2xh+h^2-x^2}{h}Förenkla täljaren
\lim\limits_{h \to 0} \frac{2xh+h^2}{h}Bryt ut h i täljaren
\lim\limits_{h \to 0} \frac{h(2x+h)}{h}Förkorta med h
\lim\limits_{h \to 0} 2x+hNu ser vi vad gränsvärdet blir:
2x då h \to 0
Alltså har f(x) = x^2 derivatan f´(x) = 2x Jämför gärna detta med deriveringsregeln för polynomfunktioner.